lecture 20: Linear regression

Prashant K

2024-02-28

Today’s class

  • Understanding (linear) relationships between 2 or more dimensions of data

    • Correlation

    • Linear regression

  • Linear regression is also useful for prediction of y (dependent variable) for new values of x (independent variable)

  • Using the lm(y ~ x, data = ?) function in R

  • Interpreting the results : Coefficients, goodness of fit, p-values

Correlation vs linear regression

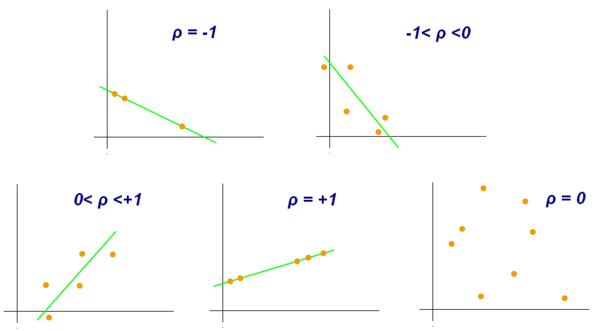
Correlation coefficient (\(\rho\)) quantifies the linearity of y ~ x (Pearson)
Spearman’s rank correlation coefficient quantifies the monotonicity (y increases when x increases)

Linear regression quantifies the slope of the linearity as well as the degree of fit (\(R^2\))

Many flavours of linear regression

  • Simple linear regression : \(y = \alpha + \beta x + \eta(0, \sigma)\)

  • Multiple linear regression: \(y = \alpha + \beta_1 x_1 + \beta_2 x_2 + ..+ \eta(0, \sigma)\)

    • regressor is non-linear, ex: polynomial regression: \(y = \alpha + \beta_1 x_1 + \beta_2 x_1^2 + ..+ \eta(0, \sigma)\)

  • Multivariate .. : multiple y values that are correlated (not statistically independent)

Fitting a straight line perfectly

Fitting a straight line between any 2 points should be easy

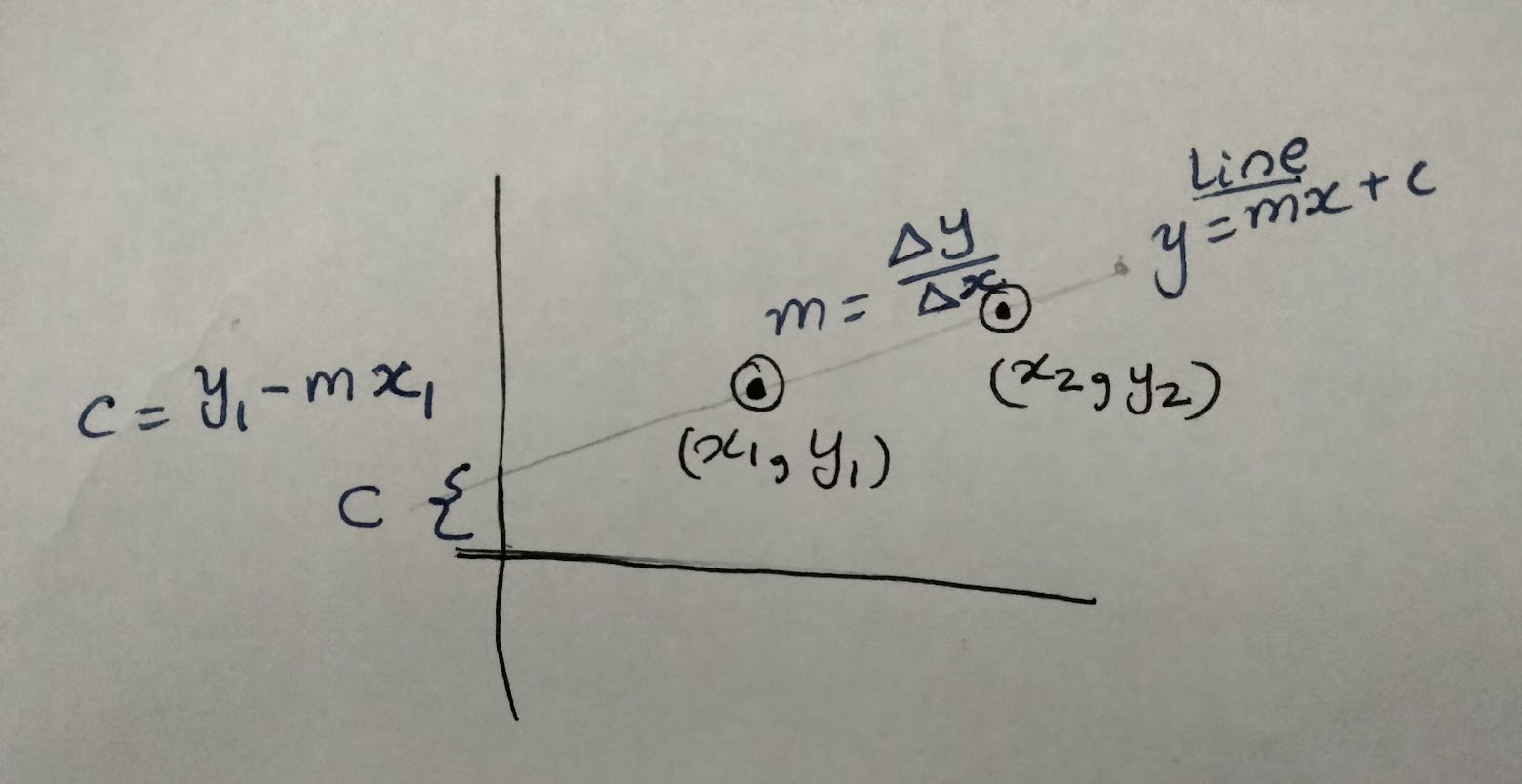
But we have noise in y, that makes this task not as straightforward

Fitting a straight line with noise

Need R to fit this numerically, using this algorithm; in R.

geom_smooth(method = 'lm') does this in the background and plots the result!

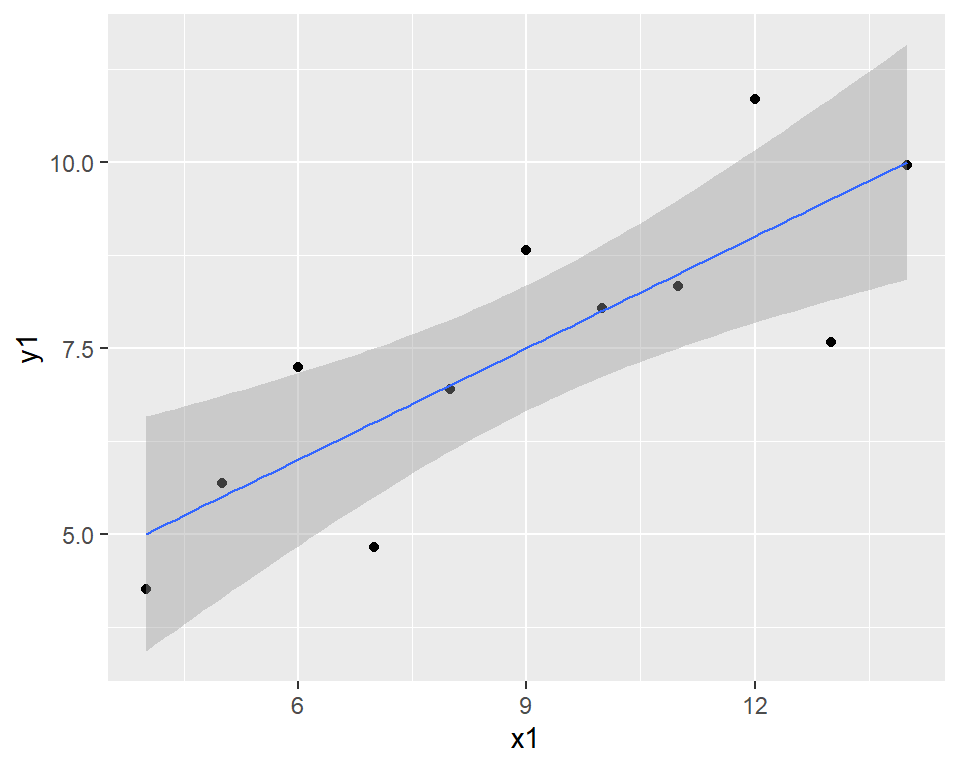
Doing linear regression in R

m <- lm(y1 ~ x1, data = anscombe) %>% print

Call:
lm(formula = y1 ~ x1, data = anscombe)

Coefficients:
(Intercept)           x1  
     3.0001       0.5001

Interpreting results of lm()

Coefficients, t-tests & goodness of fit metrics

For each coefficient, the p-values are for t-tests with null hypotheses that coefficient = 0


Call:
lm(formula = y1 ~ x1, data = anscombe)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.92127 -0.45577 -0.04136  0.70941  1.83882 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   3.0001     1.1247   2.667  0.02573 * 
x1            0.5001     0.1179   4.241  0.00217 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared:  0.6665,    Adjusted R-squared:  0.6295 
F-statistic: 17.99 on 1 and 9 DF,  p-value: 0.00217

How far are the data from fitted line?

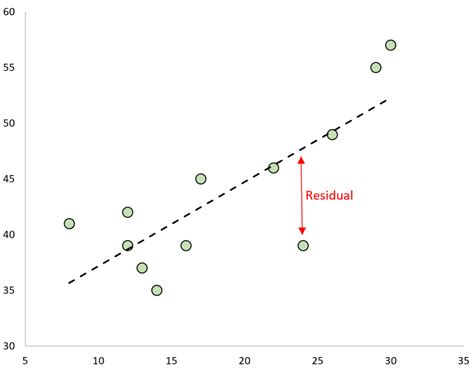
Residuals are used to see how far data is from the fitted line

QC : residuals should be normally distributed (assumption of the linear regression equation!)

Residual = observed - predicted value = \(Y_i - Y^f_i\)

Goodness of fit metrics

  • Aggregate distance of data from regression line measured by S = Std error of regression / Residual standard error = stdev(residuals)

    • Better metric. Comparable across linear and non-linear regressions!

  • \(R^2\) = % of y variance that the model explains

Let’s try these out in the worksheet

worksheet : class20-solution_linear_regression.qmd

We will follow this guide to try lm() on the mtcars data